이원배치 분산분석 (two-way ANOVA (Analysis of Variance))
이원배치 분산분석 예 (상호작용이 있는 경우)
세 종류의 캔디향 (A, B, C)와 세 가지 가격 (79센트, 89센트, 99센트)의 판매효과를 시험하려고 한다.
캔디 매출 수준이 유사한 9개의 점포를 선정하고, 판매량을 조사하였다.
| 캔디향 A | 캔디향 B | 캔디향 C | |||||||
| 79센트 | 8 | 7 | 10 | 8 | 9 | 9 | 14 | 13 | 15 |
| 89센트 | 4 | 6 | 7 | 14 | 12 | 15 | 12 | 13 | 14 |
| 99센트 | 9 | 10 | 11 | 8 | 7 | 10 | 13 | 14 | 15 |
| candy <- rep(c("apple", "grape", "lemon"), each = 9) candy |
| > candy [1] "apple" "apple" "apple" "apple" "apple" "apple" "apple" "apple" "apple" "grape" "grape" "grape" [13] "grape" "grape" "grape" "grape" "grape" "grape" "lemon" "lemon" "lemon" "lemon" "lemon" "lemon" [25] "lemon" "lemon" "lemon" |
| price <- rep(c(79, 89, 99), times = 9) price |
| > price [1] 79 89 99 79 89 99 79 89 99 79 89 99 79 89 99 79 89 99 79 89 99 79 89 99 79 89 99 |
| store <- rep(c("A", "B", "C", "E", "F", "G", "H", "I", "J"), times = 3) store |
| > store [1] "A" "B" "C" "E" "F" "G" "H" "I" "J" "A" "B" "C" "E" "F" "G" "H" "I" "J" "A" "B" "C" "E" "F" "G" [25] "H" "I" "J" |
| # 데이터프레임 생성 sales_data <- data.frame(candy, price, store, no_sales) |
| candy | price | store | no_sales |
| apple | 79 | A | 8 |
| apple | 89 | B | 4 |
| apple | 99 | C | 9 |
| apple | 79 | E | 7 |
| apple | 89 | F | 6 |
| apple | 99 | G | 10 |
| apple | 79 | H | 10 |
| apple | 89 | I | 7 |
| apple | 99 | J | 11 |
| grape | 79 | A | 8 |
| grape | 89 | B | 14 |
| grape | 99 | C | 8 |
| grape | 79 | E | 9 |
| grape | 89 | F | 12 |
| grape | 99 | G | 7 |
| grape | 79 | H | 9 |
| grape | 89 | I | 15 |
| grape | 99 | J | 10 |
| lemon | 79 | A | 14 |
| lemon | 89 | B | 12 |
| lemon | 99 | C | 13 |
| lemon | 79 | E | 13 |
| lemon | 89 | F | 13 |
| lemon | 99 | G | 14 |
| lemon | 79 | H | 15 |
| lemon | 89 | I | 14 |
| lemon | 99 | J | 15 |
상호작용이 없는 경우
[R Studio] 이원배치 분산분석 ANOVA (논문 작성을 위한 다섯 번째 분석) (tistory.com)
[R Studio] 이원배치 분산분석 ANOVA (논문 작성을 위한 다섯 번째 분석)
이원배치 분산분석 (two-way ANOVA (Analysis of Variance)) 두 가지 독립 변수 (또는 요인)가 동시에 작용하는 경우(실험)에 대한 분산분석법을 이원배치 분산분석 (two-way ANOVA)라고 한다. 이원배치 분산분
logistician.tistory.com
등분산 검증 : 루빈스 테스트 (Levene's Test)
| levene_result <- car::leveneTest(no_sales ~ candy * price, data = sales_data) print(levene_result) |
|||
| Levene's Test for Homogeneity of Variance (center = median) |
|||
| Df | F value | Pr(>F) | |
| group | 8 | 0.2647 | 0.9696 |
| 18 | |||
R / Rstudio 분산분석 (aov)
캔디향과 가격, 판매량의 분산분석(no_sales ~ candy * price)을 실행한다.
| # 분산분석 (ANOVA) model_s <- aov(no_sales ~ candy * price, data = sales_data) summary(model_s) |
||||||
| Df | Sum Sq | Mean Sq | F value | Pr(>F) | ||
| candy | 2 | 146.74 | 73.37 | 48.32 | 5.80E-08 | *** |
| price | 2 | 1.19 | 0.59 | 0.39 | 0.682 | |
| candy:price | 4 | 83.04 | 20.76 | 13.67 | 2.72E-05 | *** |
| Residuals | 18 | 27.33 | 1.52 | |||
캔디향과 가격의 상호작용효과를 보면 유의확률(0.0000)이 0.05보다 작으며,
기각하게 되어 "두 요인의 상호작용 효과는 있다."라고 할 수 있다.
상호작용이 존재하므로 각각의 요인의 효과를 따로 떼어서 분석하는 것이 불가능하며, 주효과를 독립적으로 검정할 수 없다. (더 이상 분석을 진행할 수 없음)
아래 그래프를 보면, 선들이 서로 교차되어 있는 형태를 볼 수 있다.
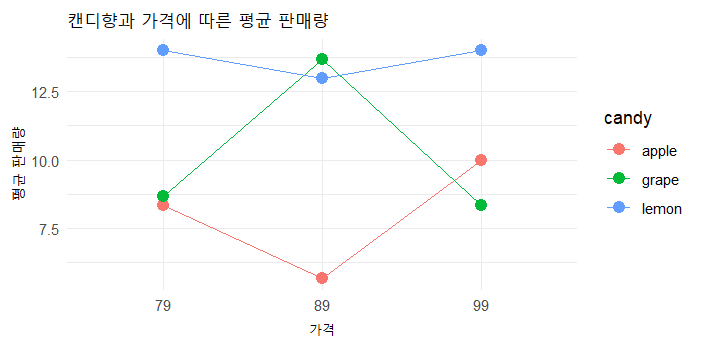
| sales_data %>% ggplot(aes(x = price, y = no_sales, group = candy)) + geom_line(stat = "summary", fun = "mean", aes(color = candy)) + geom_point(stat = "summary", fun = "mean", aes(color = candy), size=3) + labs(x = "가격", y = "평균 판매량") + ggtitle("캔디향과 가격에 따른 평균 판매량") + theme_minimal() |
상호작용 효과가 존재하면, 이 효과가 제거되도록 변수변환을 사용하도록 권하고 있지만,
상기 그래프를 볼 때, 상호작용 효과 자체가 중요한 의미를 가질 수도 있으므로 상호작용 자체를 분석할 수도 있다.
캔디향과 가격 수준의 조합을 만들면 3 X 3 = 9개의 수준 조합이 만들어진다. 9개의 집단을 나타내는 변수를 만들고, 9개 집단 간의 평균 비교를 통해서,
Tukey HSD (Honestly Significant Difference) 검정
Tukey HSD (Honestly Significant Difference)는 다중 비교를 수행하여 그룹 간의 평균 차이를 평가하고 통계적으로 유의미한 차이가 있는지를 판단하는 통계적 방법 중 하나이다.
Tukey HSD는 그룹 간 평균 차이를 비교하고 신뢰구간을 계산하여 유의미한 차이를 식별한다.
Tukey HSD는 모든 가능한 그룹 조합에 대한 평균 차이를 계산하고, 각 조합에 대한 조정된 p-value를 제공하여 모든 그룹을 서로 비교할 수 있게 한다.
| model_s <- aov(no_sales ~ candy * price, data = sales_data) TukeyHSD(model_s) |
||||
| Tukey multiple comparisons of means 95% family-wise confidence level |
||||
| Fit: aov(formula = no_sales ~ candy * price, data = sales_data) | ||||
| $candy | ||||
| diff | lwr | upr | p adj | |
| grape-apple | 2.2222220 | 0.7396624 | 3.7047820 | 0.0033752 |
| lemon-apple | 5.6666670 | 4.1841069 | 7.1492260 | 0.0000000 |
| lemon-grape | 3.4444440 | 1.9618846 | 4.9270040 | 0.0000371 |
| $price | ||||
| diff | lwr | upr | p adj | |
| 89-79 | 0.4444444 | -1.0381150 | 1.9270040 | 0.7285729 |
| 99-79 | 0.4444444 | -1.0381150 | 1.9270040 | 0.7285729 |
| 99-89 | 0.0000000 | -1.4825600 | 1.4825600 | 1.0000000 |
| $`candy:price` | ||||
| diff | lwr | upr | p adj | |
| grape:79-apple:79 | 0.3333333 | -3.1920912 | 3.8587578 | 0.9999929 |
| lemon:79-apple:79 | 5.6666670 | 2.1412422 | 9.1920912 | 0.0006422 |
| apple:89-apple:79 | -2.6666670 | -6.1920912 | 0.8587578 | 0.2328144 |
| grape:89-apple:79 | 5.3333330 | 1.8079088 | 8.8587578 | 0.0012621 |
| lemon:89-apple:79 | 4.6666670 | 1.1412422 | 8.1920912 | 0.0049619 |
| apple:99-apple:79 | 1.6666670 | -1.8587578 | 5.1920912 | 0.7633655 |
| grape:99-apple:79 | 0.0000000 | -3.5254245 | 3.5254245 | 1.0000000 |
| lemon:99-apple:79 | 5.6666670 | 2.1412422 | 9.1920912 | 0.0006422 |
| lemon:79-grape:79 | 5.3333330 | 1.8079088 | 8.8587578 | 0.0012621 |
| apple:89-grape:79 | -3.0000000 | -6.5254245 | 0.5254245 | 0.1329780 |
| grape:89-grape:79 | 5.0000000 | 1.4745755 | 8.5254245 | 0.0024977 |
| lemon:89-grape:79 | 4.3333330 | 0.8079088 | 7.8587578 | 0.0098543 |
| apple:99-grape:79 | 1.3333330 | -2.1920912 | 4.8587578 | 0.9106639 |
| grape:99-grape:79 | -0.3333333 | -3.8587578 | 3.1920912 | 0.9999929 |
| lemon:99-grape:79 | 5.3333330 | 1.8079088 | 8.8587578 | 0.0012621 |
| apple:89-lemon:79 | -8.3333330 | -11.8587578 | -4.8079088 | 0.0000044 |
| grape:89-lemon:79 | -0.3333333 | -3.8587578 | 3.1920912 | 0.9999929 |
| lemon:89-lemon:79 | -1.0000000 | -4.5254245 | 2.5254245 | 0.9816922 |
| apple:99-lemon:79 | -4.0000000 | -7.5254245 | -0.4745755 | 0.0194573 |
| grape:99-lemon:79 | -5.6666670 | -9.1920912 | -2.1412422 | 0.0006422 |
| lemon:99-lemon:79 | 0.0000000 | -3.5254245 | 3.5254245 | 1.0000000 |
| grape:89-apple:89 | 8.0000000 | 4.4745755 | 11.5254245 | 0.0000078 |
| lemon:89-apple:89 | 7.3333330 | 3.8079088 | 10.8587578 | 0.0000258 |
| apple:99-apple:89 | 4.3333330 | 0.8079088 | 7.8587578 | 0.0098543 |
| grape:99-apple:89 | 2.6666670 | -0.8587578 | 6.1920912 | 0.2328144 |
| lemon:99-apple:89 | 8.3333330 | 4.8079088 | 11.8587578 | 0.0000044 |
| lemon:89-grape:89 | -0.6666667 | -4.1920912 | 2.8587578 | 0.9987386 |
| apple:99-grape:89 | -3.6666670 | -7.1920912 | -0.1412422 | 0.0379192 |
| grape:99-grape:89 | -5.3333330 | -8.8587578 | -1.8079088 | 0.0012621 |
| lemon:99-grape:89 | 0.3333333 | -3.1920912 | 3.8587578 | 0.9999929 |
| apple:99-lemon:89 | -3.0000000 | -6.5254245 | 0.5254245 | 0.1329780 |
| grape:99-lemon:89 | -4.6666670 | -8.1920912 | -1.1412422 | 0.0049619 |
| lemon:99-lemon:89 | 1.0000000 | -2.5254245 | 4.5254245 | 0.9816922 |
| grape:99-apple:99 | -1.6666670 | -5.1920912 | 1.8587578 | 0.7633655 |
| lemon:99-apple:99 | 4.0000000 | 0.4745755 | 7.5254245 | 0.0194573 |
| lemon:99-grape:99 | 5.6666670 | 2.1412422 | 9.1920912 | 0.0006422 |
- apple:99-apple:89 (apple 99와 apple 89 두 조합 )는 유의미한 차이가 있음
- grape:89-grape:79와 grape:99-grape:89는 유의미한 차이가 있으나, grape:99-grape:79는 유의미한 차이가 없음
- lemon:89-lemon:79, lemon:99-lemon:79, lemon:99-lemon:89는 유의미한 차이가 없음
Duncan 검정 (Duncan's Multiple Range Test )
Duncan's Test와 Tukey HSD 모두 다수의 그룹 간의 평균 차이를 비교하는 데 사용된다.
Duncan's Test는 미리 정의된 그룹들 간의 비교를 수행한다. Duncan's Test는 가장 큰 평균 차이와 가장 작은 평균 차이 사이의 그룹을 찾아낸다. 이러한 그룹은 유의미한 차이를 가지며 다른 그룹과는 구분된다.
Duncan's Test는 큰 평균 차이에 대해서만 강조되며, Tukey HSD보다 상대적으로 더 높은 유의수준을 요구한다.
| sales_data$candy_price <- paste0(candy, "+", price) model_n <- aov(no_sales ~candy_price, data = sales_data) summary(model_n) duncan.test(model_n, "candy_price", console = T, alpha = 0.05) |
|||||||||
| Study: model_n ~ "candy_price" | |||||||||
| Duncan's new multiple range test |
|||||||||
| for no_sales | |||||||||
| Mean Square Error: 1.518519 | |||||||||
| candy_price, means | |||||||||
| no_sales | std | r | se | Min | Max | Q25 | Q50 | Q75 | |
| apple+79 | 8.333333 | 1.527525 | 3 | 0.711458 | 7 | 10 | 7.5 | 8 | 9 |
| apple+89 | 5.666667 | 1.527525 | 3 | 0.711458 | 4 | 7 | 5 | 6 | 6.5 |
| apple+99 | 10 | 1 | 3 | 0.711458 | 9 | 11 | 9.5 | 10 | 10.5 |
| grape+79 | 8.666667 | 0.57735 | 3 | 0.711458 | 8 | 9 | 8.5 | 9 | 9 |
| grape+89 | 13.66667 | 1.527525 | 3 | 0.711458 | 12 | 15 | 13 | 14 | 14.5 |
| grape+99 | 8.333333 | 1.527525 | 3 | 0.711458 | 7 | 10 | 7.5 | 8 | 9 |
| lemon+79 | 14 | 1 | 3 | 0.711458 | 13 | 15 | 13.5 | 14 | 14.5 |
| lemon+89 | 13 | 1 | 3 | 0.711458 | 12 | 14 | 12.5 | 13 | 13.5 |
| lemon+99 | 14 | 1 | 3 | 0.711458 | 13 | 15 | 13.5 | 14 | 14.5 |
| Alpha: 0.05 ; DF Error: 18 |
|||||||||
| Critical Range | |||||||||
| 2 | 3 | 4 | 5 | 6 | 7 | 8 | 9 | ||
| 2.113851 | 2.217889 | 2.283536 | 2.329024 | 2.362274 | 2.387406 | 2.406822 | 2.422036 | ||
| Means with the same letter are not significantly different. |
|||||||||
| no_sales | groups | ||||||||
| lemon+79 | 14.00000 | a | |||||||
| lemon+99 | 14.00000 | a | |||||||
| grape+89 | 13.66667 | a | |||||||
| lemon+89 | 13.00000 | a | |||||||
| apple+99 | 10.00000 | b | |||||||
| grape+79 | 8.66667 | b | |||||||
| apple+79 | 8.33333 | b | |||||||
| grape+99 | 8.33333 | b | |||||||
| apple+89 | 5.66667 | c | |||||||
- apple의 가격 조합인 apple+99와 apple+79의 "groups" 열은 모두 'b'로 통계적으로 유의미한 차이가 없음
- grape의 가격 조합인 grape+89의 "groups" 열만 'a'이고 grape+79와 grape+99는 'b'로 두 그룹 간 차이가 있음
- lemon의 가격 조합인 lemon+79, lemon+99, lemon+89의 "groups" 열은 모두 'a'로 통계적으로 유의미한 차이가 없음
| 99 (apple+99) *10 + 89 (grape+89) * 13.66667 + 99 (lemon+99) *14 = 3592.334 |
| 99 (apple+99) *10 + 99 (grape+99) * 8.33333 + 99 (lemon+99) *14 = 3201 |
Tukey HSD 검정 결과와 Duncan 검정 결과를 고려할 때,
Apple은 99센트, Grape는 89센트, Lemon은 99센트에 판매하는 것이 최적의 방안으로 선택할 수 있다.
'데이터 분석 (with Rstudio)' 카테고리의 다른 글
| [R studio] 작업 디렉터리 (디렉토리, 폴더) 확인, 설정 변경 관리 (0) | 2023.10.07 |
|---|---|
| [R Studio] 비모수 검정과 사후 분석 (논문 작성을 위한 여섯 번째 분석) (1) | 2023.10.02 |
| [R Studio] 이원배치 분산분석 ANOVA (논문 작성을 위한 다섯 번째 분석) (0) | 2023.10.01 |
| [R Studio] 평균의 비교 대응 표본 T-검정(test) (논문 작성을 위한 네 번째 분석) (0) | 2023.09.28 |
| [R Studio] 평균의 비교 T-검정(test) (논문 작성을 위한 네 번째 분석) (0) | 2023.09.28 |



