비모수 검정 (Nonparametric Test)
모수적 방법 (Parametric method)은 관측값이 어느 특정한 확률분포 (정규분포, 이항분포 등)를 따른다고 전제를 한 후, 그 분포의 모수 (Parameter)에 대한 검정을 실시하는 방법이다.
반면에, 비모수 검정(Nonparametric Test)은 모집단의 분포에 대한 가정이나 정규 분포 가정을 만족하지 않는 데이터에 대한 통계적 가설 검정 방법이다. 비모수 검정은 데이터의 분포에 대한 가정이 덜 필요하거나 없어도 되며, 주로 순위 또는 순서에 의한 비교를 통해 통계적 추론을 수행한다.
[비모수 검정 예시 1 : 의학 분야 - 치료 효과 평가]
어떤 신약이 특정 질병의 치료에 효과적인지 비교하려면 환자 그룹 간의 중위수 차이를 비교하는 Mann-Whitney U Test를 사용할 수 있다.
[비모수 검정 예시 2 : 가정 의학/보건 분야 - 생활습관과 건강 분석]
운동, 커피, 흡연 등의 생활습관과 건강 상태 간의 관련성을 평가할 때 사용될 수 있다. 예를 들어, 흡연자와 비흡연자 간의 어떤 건강 지표의 중위수 차이를 비교하여 흡연이 건강에 미치는 영향을 분석할 수 있다.
[비모수 검정 예시 3 : 사회과학 분야 - 설문 조사 분석]
설문 조사 후, 두 그룹 간에 어떤 사회적 현상에 대한 태도가 다른지 비교하거나, 설문 조사 결과를 비교하는 데에 활용된다.
[비모수 검정 예시 4 : 환경 과학 분야 - 환경 영향 분석]
환경 연구에서는 종종 환경 조건이나 오염 물질 노출에 따른 생물학적 효과를 평가한다. 이때 비모수 검정을 사용하여 노출 그룹과 비노출 그룹 간의 중위수 차이를 비교하여 영향을 평가할 수 있다.
[비모수 검정 예시 5 : 비즈니스 분야 - 제품 선호도 비교]
서로 다른 두 제품의 소비자 선호도를 파악하거나 제품의 품질 변화를 모니터링하는 데에 활용됩니다.
비모수 검정은 일반적으로 모수 검정보다 검정 능력이 떨어진다. 따라서, 비모수 검정은 데이터의 분포를 정확히 모를 때 또는 정규 분포를 가정하기 어려운 경우에 사용한다.
독립 표본의 Mann-Whitney U Test
(또는 Wilcoxon Rank Sum Test)
비모수 검정 중에서도 가장 일반적인 것 중 하나인 Mann-Whitney U Test (또는 Wilcoxon Rank Sum Test)는 두 독립적인 그룹 간의 중위수 비교에 사용된다.
Mann-Whitney U Test와 Wilcoxon Rank Sum Test는 정확하게는 서로 다른 용어로 상황에 따라 다르게 불리기도 하지만, 기본적으로는 동일한 비모수적인 두 그룹 간의 중위수 차이를 검정하는 방법으로, 서로 교환해서 사용한다.
wilcox.test() 함수를 사용한다.
흡연이 운전 실력에 미치는 영향을 평가하기 위하여 운전습관, 주의력, 속도감 등을 점수화한 결과가 다음과 같다고 할 때, 두 집단 사이의 운전 실력에 차이가 있는지 검정(비모수 검정)을 하고자 한다.
| 흡연자 | 28 | 53 | 39 | 27 | 41 | 68 | 27 | 28 | 45 | 48 | 65 | 78 | ||
| 비흡연자 | 32 | 35 | 61 | 43 | 82 | 44 | 78 | 38 | 85 | 63 | 46 | 30 | 47 | 57 |
| smoker <- c(28, 53, 39, 27, 41, 68, 27, 28, 45, 48, 65, 78) non_smoker <- c(32, 35, 61, 43, 82, 44, 78, 38, 85, 63, 46, 30, 47, 57) # Mann-Whitney U Test 실행 wilcox.test(smoker, non_smoker) |
| > wilcox.test(smoker, non_smoker) Wilcoxon rank sum test with continuity correction data: smoker and non_smoker W = 63.5, p-value = 0.118 alternative hypothesis: true location shift is not equal to 0 Warning message: In wilcox.test.default(smoker, non_smoker) : tie가 있어 정확한 p값을 계산할 수 없습니다 |
- Mann-Whitney U Test 통계량은 63.5이며, p-값 (p-value)이 유의수준 0.05보다 크므로 귀무가설은 기각할 수 없다.
- "흡연자와 비흡자 집단 사이의 운전 기술의 차이가 없다."라고 판단한다.
Wilcoxon 부호 순위 검정 (Wilcoxon Signed-Rank Test)
Wilcoxon 부호 순위 검정(Wilcoxon Signed-Rank Test)은 두 관련 그룹 간의 차이를 비교하는 비모수 검정 방법 중 하나이다. 이 검정은 두 관련 그룹의 데이터가 서로 독립적이지 않을 때 사용되며, 주로 대응 표본 또는 짝지어진 표본 간의 차이를 평가하는 데 사용됩니다.
두 생산라인 '라인 1'과 '라인 2'에서 생산된 제품을 10일 동안 관측한 결과, 각 생산라인의 일별 불량품의 수가 아래와 같이 관측되었다. 두 생산라인의 일별 생산량이 동일하다고 할 때, 두 생산라인에서 생산된 제품 중에서 불량품 수의 분포가 동일한가를 검정하고자 한다.
- 귀무가설 : 두 생산라인의 일별 생산량 중 불량품의 수의 분포는 동일하다.
- 대립가설 : 두 생산라인의 일별 생산량 중 불량품의 수의 분포는 동일하지 않다.
| 일자 | 1 | 2 | 3 | 4 | 5 | 6 | 7 | 8 | 9 | 10 |
| 라인1 | 170 | 179 | 140 | 184 | 174 | 142 | 191 | 169 | 161 | 200 |
| 라인2 | 201 | 164 | 159 | 195 | 177 | 170 | 183 | 179 | 170 | 212 |
| line_1 <- c(170, 179, 140, 184, 174, 142, 191, 169, 161, 200) line_2 <- c(201, 164, 159, 195, 177, 170, 183, 179, 170, 212) # Wilcoxon 부호 순위 검정 실행 wilcox.test(line_1, line_2, paired = TRUE) |
| > wilcox.test(line_1, line_2, paired = TRUE) Wilcoxon signed rank exact test data: line_1 and line_2 V = 9, p-value = 0.06445 alternative hypothesis: true location shift is not equal to 0 |
- p-값 (p-value)이 유의수준 0.05보다 크므로 귀무가설은 기각할 수 없다.
- 두 생산라인의 일별 생산량 중, 불량품 수의 분포는 동일하다는 결론을 내일 수 있다.
| # 두 분포의 차이 계산 difference <- line_2 - line_1 # 음수, 양수, 0으로 분리 negative_diff <- difference[difference < 0] #difference 벡터 중에서 음수인 값을 선택 zero_diff <- difference[difference == 0] #difference 벡터 중에서 0인 값을 선택 positive_diff <- difference[difference > 0] #difference 벡터 중에서 양수인 값을 선택 negative_diff zero_diff positive_diff |
| > negative_diff [1] -15 -8 > zero_diff numeric(0) > positive_diff [1] 31 19 11 3 28 10 9 12 |
| # 음수, 양수, 0인 경우를 각각 정리 count_negative <- length(negative_diff) count_zero <- length(zero_diff) count_positive <- length(positive_diff) count_negative count_zero count_positive |
| > count_negative [1] 2 > count_zero [1] 0 > count_positive [1] 8 |
Kruskal-Wallis의 일원배치 분산분석
Kruskal-Wallis 일원배치 분산분석은 비모수적인 방법으로 데이터의 그룹 간에 통계적으로 유의미한 차이가 있는지를 검정하는 통계적 방법이다.
이 분석은 일반적으로 등분산성을 가정하지 않고, 데이터가 정규 분포를 따르지 않아도 적용할 수 있다.
주로 다음과 같은 상황에서 사용됩니다.
- 그룹 간의 평균 비교: Kruskal-Wallis 검정은 세 개 이상의 그룹 간의 평균 비교를 수행하는 데 사용된다.
예를 들어, 세 가지 다른 약물 치료법의 효과를 비교하려는 경우에 적용할 수 있다. - 범주형 데이터: 범주형 데이터 또는 순서형 데이터에 대한 비모수적인 비교를 위해 사용된다.
Kruskal-Wallis 검정은 다음과 같은 가설을 검정한다
- 귀무 가설 (H0): 모든 그룹의 분포는 동일하다.
- 대립 가설 (H1): 적어도 하나의 그룹은 다른 그룹들과 분포가 다르다.
만약 Kruskal-Wallis 검정 결과에서 귀무 가설을 기각한다면, 적어도 하나의 그룹 간에 통계적으로 유의미한 차이가 있음을 나타낸다. 이후 다변량 비교 분석을 통해 어떤 그룹 간에 차이가 있는지를 식별할 수 있다.
세 가지 다른 브랜드의 커피를 비교하여, 어떤 브랜드의 커피가 소비자들의 만족도에 영향을 미치는지를 알고자 한다. 만족도는 1부터 10까지의 순서형 데이터로 측정되었다.
| 브랜드 | 만족도 | |||||||||
| A | 8 | 7 | 6 | 6 | 7 | 8 | 7 | 6 | 6 | 7 |
| B | 9 | 8 | 7 | 7 | 8 | 9 | 8 | 7 | 7 | 8 |
| C | 6 | 5 | 4 | 5 | 5 | 6 | 5 | 4 | 5 | 5 |
| brand_A <- c(8, 7, 6, 6, 7, 8, 7, 6, 6, 7) brand_B <- c(9, 8, 7, 7, 8, 9, 8, 7, 7, 8) brand_C <- c(6, 5, 4, 5, 5, 6, 5, 4, 5, 5) # 데이터를 하나의 벡터로 합치기 coffee_data <- c(brand_A, brand_B, brand_C) coffee_data # 브랜드 정보 생성 brands <- rep(c("A", "B", "C"), each = 10) # 데이터프레임 생성 coffee_df <- data.frame(Brand = brands, Satisfaction = coffee_data) # Kruskal-Wallis 검정 수행 kruskal_test_result <- kruskal.test(Satisfaction ~ Brand, data = coffee_df) # 결과 출력 print(kruskal_test_result) |
| > print(kruskal_test_result) Kruskal-Wallis rank sum test data: Satisfaction by Brand Kruskal-Wallis chi-squared = 21.389, df = 2, p-value = 2.267e-05 |
- Kruskal-Wallis chi-squared 값 (21.389)은 검정 통계량을 나타냅니다. 이 값은 데이터셋의 브랜드 간에 만족도에 대한 차이를 나타낸다. 검정 통계량이 높을수록 그룹 간 차이가 크다는 것을 의미한다.
- 자유도 (df)는 검정에 사용된 그룹의 수에서 1을 뺀 값이다. 여기서는 3개의 브랜드가 있으므로 df는 2이다.
- p-value (2.267e-05)은 귀무 가설을 검정한 결과이다. 이 p-value는 유의수준 0.05보다 훨씬 작으므로 귀무 가설을 기각할 충분한 증거가 있다. 따라서 이 결과로부터 세 가지 다른 브랜드의 커피 만족도 간에 통계적으로 유의미한 차이가 있다는 결론을 내릴 수 있다.
즉, 적어도 하나의 브랜드의 커피 만족도가 다른 브랜드와 유의미하게 다르다는 것을 나타낸다.
R / Rstudio 사후 분석 (사후 검정, Post hoc test)
Kruskal-Wallis 검정을 통해 그룹 간에 차이가 있는 것을 확인했다면, 이후에 어떤 그룹 간에 차이가 있는지를 더 자세히 식별하려면 다변량 비교 분석을 수행할 수 있다. 다변량 비교 분석을 수행하는 일반적인 방법 중 하나는 사후 검정(Post hoc test)을 사용하는 것이다.
Kruskal-Wallis 검정에서는 그룹 간의 차이가 있다는 일반적인 결과만 얻을 수 있고, 어느 그룹이 다른 그룹과 다른지에 대한 구체적인 정보는 얻을 수 없다. 따라서 사후 검정을 통해 각 그룹 간에 차이를 확인할 수 있다.
Dunn의 검정 #1 (Dunn's Test)
다중 비교를 위해 사용되며, 데이터의 순위를 기반으로 한다.
세 그룹 이상의 집단 비교에서 효과적이다.
Bonferroni 보정, Holm 보정 등 다양한 보정 방법을 사용할 수 있다.
| # 패키지 설치: install.packages("dunn.test") install.packages('dunn.test') library(dunn.test) # 데이터 변환 data_to_test <- list(brand_A, brand_B, brand_C) # Dunn's 검정 수행 dunn.test(data_to_test, method = "bonferroni") |
| Kruskal-Wallis rank sum test data: data_to_test and group Kruskal-Wallis chi-squared = 21.3888, df = 2, p-value = 0 Comparison of data_to_test by group (Bonferroni)  alpha = 0.05 Reject Ho if p <= alpha/2 |
Kruskal-Wallis 검정 결과
- Kruskal-Wallis chi-squared 값: 21.3888
- 자유도 (df): 2
- p-value: 0
- Kruskal-Wallis 검정의 결과로, 그룹 간에는 통계적으로 유의한 차이가 있음을 나타낸다.
- 즉, 적어도 한 그룹은 다른 그룹들과 다른 평균을 가지고 있다.
Dunn's 검정 결과 (Bonferroni 수정)
- 각 그룹 쌍에 대한 비교 결과가 나타나 있다. 두 그룹 간의 평균 차이와 해당 비교의 p-value가 표시된다.
- 비교된 그룹: 1과 2 그룹, 2와 3 그룹
- 평균 차이 (Col Mean-Row Mean): 위쪽 숫자
- p-value: 아래쪽 숫자
- 1과 2 그룹 비교:
- 평균 차이: -1.661280 (평균 차이가 -1.661280으로 음수)
- p-value: 0.1450
- p-value는 0.1450으로 유의수준인 alpha(일반적으로 0.05)보다 크므로 귀무 가설을 기각하지 않는다.
- 즉, 1과 2 그룹 사이에는 통계적으로 유의한 차이가 없다.
- 1와 3 그룹 비교:
- 평균 차이: 2.907240 (평균 차이가 2.907240으로 양수)
- p-value: 0.0055*
- p-value는 0.0055로 유의수준인 alpha보다 작으므로 귀무 가설을 기각한다.
- 즉, 1과 3 그룹 사이에는 통계적으로 유의한 차이가 있다.
- 2와 3 그룹 비교:
- 평균 차이: 4.568520 (평균 차이가 4.568520으로 양수)
p-value: 0.0000*
p-value는 0.0000으로 유의수준인 alpha보다 작으므로 귀무 가설을 기각한다.
즉, 2와 3 그룹 사이에는 통계적으로 유의한 차이가 있다.
- 평균 차이: 4.568520 (평균 차이가 4.568520으로 양수)
- 1과 3그룹간과 2와 3 그룹 간에는 통계적으로 유의한 차이가 있으며, 1과 2 그룹 간에는 차이가 없다는 결론을 내릴 수 있다.
- 브랜드 A (그룹 1)와 브랜드 C (그룹 3) 간에는 통계적으로 유의한 차이가 있다. 브랜드 B (그룹 2)와 브랜드 C (그룹 3) 간에도 통계적으로 유의한 차이가 있다. 그러나 브랜드 A (그룹 1)와 브랜드 B (그룹 2) 간에는 통계적으로 유의한 차이가 없다.
대다수의 참가자들은 브랜드 A와 브랜드 B를 선호하는 데에는 큰 차이가 없으나, 브랜드 C는 브랜드 A와 B와 비교하여 선호되는 경향이 다르다.
Dunn의 검정 #2 (Dunn's Test)
| # 필요한 패키지를 설치하고 라이브러리를 불러옵니다. install.packages("DescTools") library("DescTools") # Dunn Test DunnTest(Satisfaction ~ Brand, data = coffee_df) |
Dunn's test of multiple comparisons using rank sums : holm 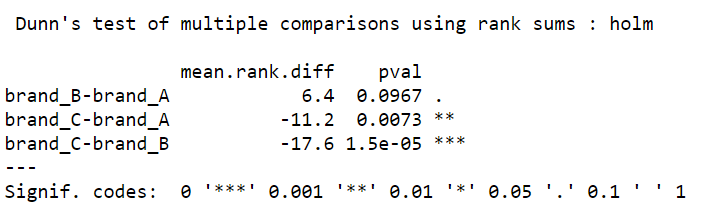 --- Signif. codes: 0 '***' 0.001 '**' 0.01 '*' 0.05 '.' 0.1 ' ' 1 |
- brand_B와 brand_A 간의 선호도 차이:
- 평균 순위 차이는 6.4이며, p-value는 0.0967아다. 유의수준 0.05에서 평균 순위 차이가 유의미하지 않다.
- 따라서 브랜드 B와 브랜드 A 간의 선호도 차이는 통계적으로 유의미하지 않다고 할 수 있다.
- brand_C와 brand_A 간의 선호도 차이:
- 평균 순위 차이는 -11.2이며, p-value는 0.0073이다. 유의수준 0.05에서 평균 순위 차이가 유의미하다.
- 따라서 브랜드 C와 브랜드 A 간의 선호도 차이는 통계적으로 유의미하다고 할 수 있다.
- brand_C와 brand_B 간의 선호도 차이:
- 평균 순위 차이는 -17.6이며, p-value는 1.5e-05 (0.000015)이다. 유의수준 0.05에서 평균 순위 차이가 매우 유의미하다.
- 따라서 브랜드 C와 브랜드 B 간의 선호도 차이는 통계적으로 매우 유의미하다고 할 수 있다.
- 결론적으로, Dunn's Test 결과를 통해 브랜드 A, B, C 간의 선호도를 비교한 결과, 브랜드 C와 브랜드 A 간, 그리고 브랜드 C와 브랜드 B 간의 선호도 차이가 통계적으로 유의미하며, 특히 브랜드 C와 브랜드 B 간의 차이가 가장 크게 나타났음을 알 수 있다.
Pairwise Wilcoxon Test
두 그룹 간의 비교가 주요 관심사일 때 사용한다.
각 조합마다 별도의 Wilcoxon rank sum test를 수행하므로 많은 비교가 필요할 때는 보정이 필요하다.
각 비교에 대한 p-값을 확인하고자 할 때 유용하다.
| # 데이터프레임 생성 coffee_df <- data.frame( Brand = rep(c("brand_A", "brand_B", "brand_C"), each = 10), Satisfaction = c(brand_A, brand_B, brand_C) ) # Pairwise Wilcoxon Test pairwise.wilcox.test(coffee_df$Satisfaction, coffee_df$Brand, p.adjust.method = "bonferroni", correct = FALSE) |
| Pairwise comparisons using Wilcoxon rank sum test data: coffee_df$Satisfaction and coffee_df$Brand brand_A brand_B brand_B 0.05089 - brand_C 0.00099 0.00033 P value adjustment method: bonferroni |
- brand_A와 brand_B 간의 선호도 비교:
- p-value는 0.05089로 이 값은 브랜드 A와 브랜드 B 간의 선호도 차이가 통계적으로 유의미하지 않다는 것을 나타낸다.
- 즉, 브랜드 A와 브랜드 B의 선호도가 유사하다고 할 수 있다.
- brand_A와 brand_C 간의 선호도 비교:
- p-value는 0.00099로 이 값은 브랜드 A와 브랜드 C 간의 선호도 차이가 통계적으로 매우 유의미하다는 것을 나타낸다.
- 즉, 브랜드 A와 브랜드 C의 선호도가 다르다고 할 수 있다.
- brand_B와 brand_C 간의 선호도 비교:
- p-value는 0.00033으로 이 값은 브랜드 B와 브랜드 C 간의 선호도 차이가 통계적으로 매우 유의미하다는 것을 나타낸다.
- 즉, 브랜드 B와 브랜드 C의 선호도가 다르다고 할 수 있습니다.
Conover Test
Dunn's Test와 유사하게 데이터의 순위를 기반으로 다중 비교 분석을 수행한다.
세 그룹 이상의 집단 비교에서 효과적이다.
| ConoverTest(Satisfaction ~ Brand, data = coffee_df) |
Conover's test of multiple comparisons : holm  --- Signif. codes: 0 '***' 0.001 '**' 0.01 '*' 0.05 '.' 0.1 ' ' 1 |
Nemenyi Test
세 그룹 이상의 집단 비교에서 효과적이며, Nemenyi Test는 Holm 보정을 포함한 다양한 보정 방법을 지원한다.
| NemenyiTest(Satisfaction ~ Brand, data = coffee_df) |
Nemenyi's test of multiple comparisons for independent samples (tukey)  --- Signif. codes: 0 '***' 0.001 '**' 0.01 '*' 0.05 '.' 0.1 ' ' 1 |

Pixabay로부터 입수된 kalhh님의 이미지 입니다.
'데이터 분석 (with Rstudio)' 카테고리의 다른 글
| [R studio] 다른 디렉터리 (디렉토리, 폴더) 파일 불러오기 저장하기 (0) | 2023.10.07 |
|---|---|
| [R studio] 작업 디렉터리 (디렉토리, 폴더) 확인, 설정 변경 관리 (0) | 2023.10.07 |
| [R Studio] 이원배치 분산분석 ANOVA 2 (상호작용이 있는 경우) (1) | 2023.10.01 |
| [R Studio] 이원배치 분산분석 ANOVA (논문 작성을 위한 다섯 번째 분석) (0) | 2023.10.01 |
| [R Studio] 평균의 비교 대응 표본 T-검정(test) (논문 작성을 위한 네 번째 분석) (0) | 2023.09.28 |



