반응형
기술통계 (Descriptive Statistics)
기술통계는 영어명에서 보는 것 처럼, 우리가 흔히 말하는 기술 [技術]이 아닌, 기록하여 서술한다는 의미의 기술 [記述] 임
- 기술통계란 데이터를 요약, 표현, 해석하는 방법으로, 데이터의 특성과 패턴을 이해하는 데 도움이 되는 통계적인 기법
- 기술통계는 주어진 데이터를 요약하여 중심 경향성(평균, 중앙값, 최빈값 등)과 분산, 분포 등의 특성을 파악
- 주로 평균, 중앙값, 표준편차, 최소값, 최대값, 분위수 등을 계산하여 데이터의 기본 특성을 파악
| 기술 [記述] : 사물의 내용을 기록하여 서술함 기술하다 [記述--] : (사람이 사물의 내용을) 기록하여 서술하다. (사람이나 책이 사물의 내용을 어떤 방식으로) 서술하거나 설명하다. (사람이나 책 따위가 어떠하다고) 기록하여 서술하다. describe : 1. 묘사하다2. 설명하다3. 표현하다4. 기술하다5. 그리다 descriptive : 1. 기술적인2. 서술적인3. 서사적4. 묘사하는5. 설명적인 |
| 기술 [技術] : 어떤 원리나 지식을 자연적 대상에 적용하여 인간 생활에 유용하도록 만드는 구체적이고 실제적인 수단 |
Slam Dunk 데이터에서 summary라는 함수를 활용하여, height의 사분위수와 중앙값, 평균을 파악함
| summary(slam_dunk$height) #특정 필드만 적용 |
Min. 1st Qu. Median Mean 3rd Qu. Max.
162.0 169.5 174.5 176.7 184.8 197.0 summary 함수를 이용하여 요약 자료를 파악할 수도 있으나, 기술통계의 각 값을 R함수를 사용하여 계산할 수 있음
평균 : mean
| # 평균 계산 mean_value <- mean(slam_dunk$height) print(paste("평균:", mean_value)) |
[1] "평균: 176.666666666667"상북고 농구부의 평균 신장은 176.7cm로 분석됨
중앙값 : median
| # 중앙값 계산 median_value <- median(slam_dunk$height) print(paste("중앙값:", median_value)) |
[1] "중앙값: 174.5"상북고 농구부의 신장 중앙값은 174.5cm로 분석됨

| 상기 데이터 height를 오름차순(작은 값부터 끝 값 순서)로 정렬하면 162 164 168 170 170 171 178 180 184 187 189 197 이며 데이터가 12개 이므로, 가운데 5번째와 6번째의 값인 171과 178을 2로 나누면, 174.5가 중앙값이 됨 |
데이터의 개수에 따라 중앙값을 구하는 방법은 다르게 적용됨
- 데이터 개수가 홀수인 경우의 중앙값 산출
- 중앙값은 데이터를 크기순으로 정렬했을 때 가장 가운데에 위치한 값
- 예를 들어, 데이터가 {3, 1, 4, 2, 5}인 경우, 중앙값은 3이 됨
- 데이터의 개수가 홀수이므로 정렬한 후에 정확히 가운데 위치한 값이 중앙값이 됨
- 데이터 개수가 짝수인 경우의 중앙값 산출
- 중앙값은 데이터를 크기순으로 정렬했을 때 가장 가운데에 위치한 두 값의 평균으로 구함
- 예를 들어, 데이터가 {3, 1, 4, 2}인 경우, 중앙값은 (2 + 3) / 2 = 2.5
- 데이터의 개수가 짝수이므로 정렬한 후에 가운데 두 값의 평균이 중앙값이 됨
최빈값
| # 최빈값 계산 mode_value <- table(slam_dunk$height) mode_value <- as.numeric(names(mode_value[mode_value == max(mode_value)])) print(paste("최빈값:", mode_value)) |
[1] "최빈값: 170"- R 기본 라이브러리에는 최빈값을 구하는 mode 함수가 없기 때문에, table 함수로 빈도를 산출한 후, 빈도가 가장 많은 Factor를 반환하도록 함
- 'DescTools'를 설치하면, Mode 함수를 이용하여, 최빈값을 구할 수 있음
| # 예시 데이터 1 data1 <- c(1, 2, 3, 2, 2, 4, 5, 2) # 최빈값 계산 mode_value1 <- Mode(data1) # 결과 출력 print(mode_value1) |
# 예시 데이터 2 data2 <- c(1, 2, 3, 2, 3, 4, 5, 4) # 최빈값 계산 mode_value2 <- Mode(data2) # 결과 출력 print(mode_value2) |
| [1] 2 attr(,"freq") [1] 4 |
[1] 2 3 4 attr(,"freq") [1] 2 |
- 예시 데이터 1의 최빈값은 2로 4개가 있음
- 예시 데이터 2의 최빈값은 2, 3, 4로 각 2개씩 있음
표준편차 : sd
| # 표준편차 계산 sd_value <- sd(slam_dunk$height) print(paste("표준편차:", sd_value)) |
[1] "표준편차: 10.9156545910685"분산 : var
| # 분산 계산 var_value <- var(slam_dunk$height) print(paste("분산:", var_value)) |
[1] "분산: 119.151515151515"최소값 : min
| # 최소값 계산 min_value <- min(slam_dunk$height) print(paste("최소값:", min_value)) |
[1] "최소값: 162"최대값 : max
| # 최대값 계산 max_value <- max(slam_dunk$height) print(paste("최대값:", max_value)) |
[1] "최대값: 197"사분위수 : quantile
| # 사분위수 계산 quantile_values <- quantile(slam_dunk$height, probs = c(0.25, 0.5, 0.75)) print("사분위수:") print(quantile_values) |
25% 50% 75%
169.50 174.50 184.75 데이터의 분포와 분포 모양 확인
데이터의 분포와 특성을 파악하기 위해서 기술통계를 산출하나, 데이터가 많은 경우는 특성을 파악하기 어렵기 때문에
히스토그램, 박스 플롯(Box Plot) 등을 사용하여, 데이터의 모양, 이상치, 분산 등을 시각적으로 파악
히스토그램
- 데이터를 구간별로 나누어 각 구간에 속하는 데이터 개수를 막대로 표시하는 그래프
- 데이터의 분포 모양을 파악하는데 유용하며, 데이터의 빈도와 밀집도를 시각화할 수 있음
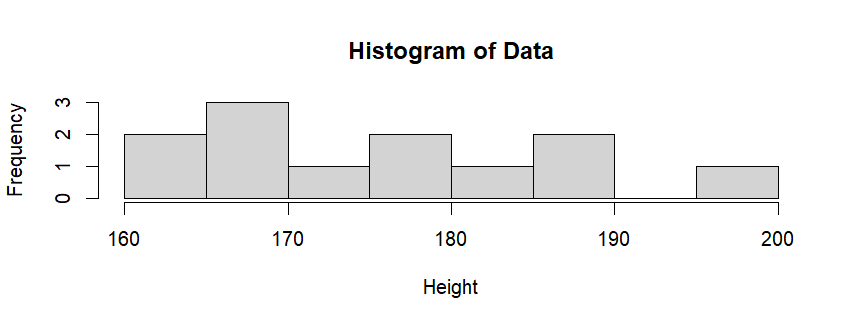
| hist(slam_dunk$height) # hist 함수 사용 |
| library(tidyverse) ggplot (slam_dunk, aes(x=height)) + geom_histogram() # ggplot 과 geom_histogram 사용 |
── Attaching packages ─────────────────────────────────────────────── tidyverse 1.3.1 ──
✔ ggplot2 3.3.6 ✔ purrr 0.3.4
✔ tibble 3.1.7 ✔ dplyr 1.0.9
✔ tidyr 1.2.0 ✔ stringr 1.4.0
✔ readr 2.1.2 ✔ forcats 0.5.1
── Conflicts ────────────────────────────────────────────────── tidyverse_conflicts() ──
✖ dplyr::filter() masks stats::filter()
✖ dplyr::lag() masks stats::lag()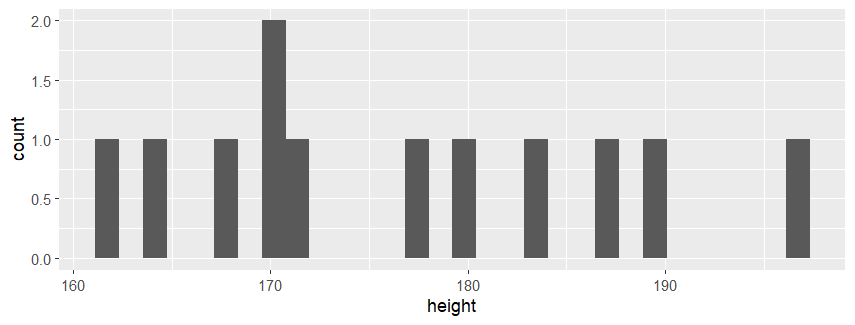
- 히스토그램을 통해서 상북고 농구부의 신장별 선수 수 분포를 파악할 수 있음
박스 플롯
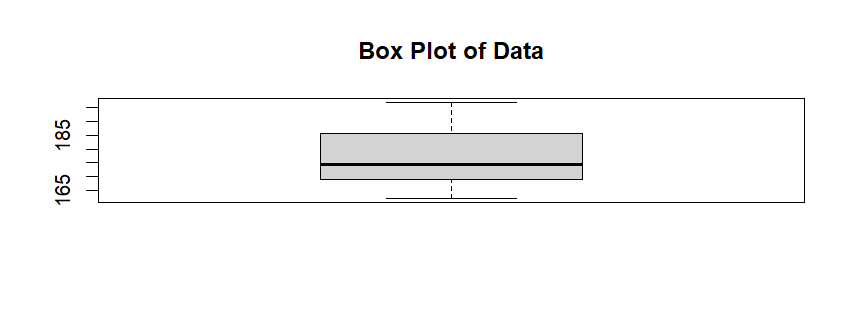
- 데이터의 중앙값, 사분위수(25%, 50%, 75%), 이상치 등을 시각적으로 표현하는 그래프
- 데이터의 분포를 빠르게 파악할 수 있고, 이상치를 확인하는 데 유용
| boxplot(slam_dunk$height, main = "Box Plot of Data") # boxplot 함수 사용 |
| ggplot (slam_dunk, aes(y=height)) + geom_boxplot() # ggplot 과 geom_boxplot 사용 (height가 y축) |
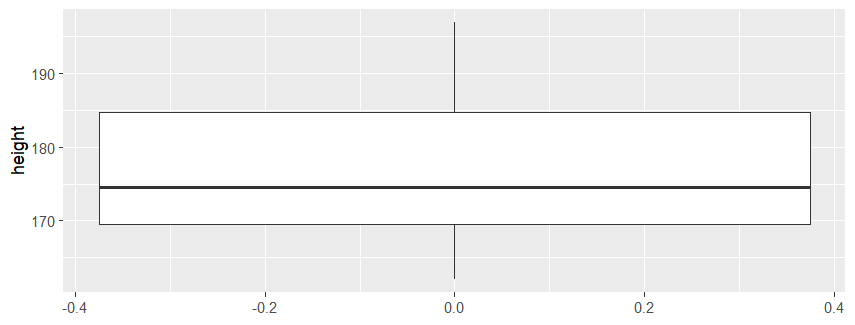
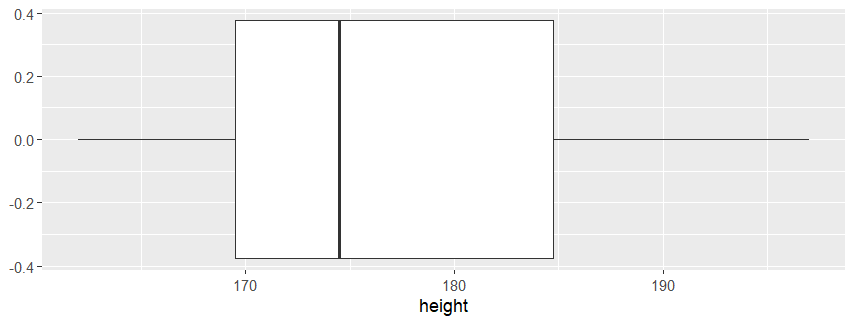
| ggplot (slam_dunk, aes(x=height)) + geom_boxplot() # ggplot 과 geom_boxplot 사용 (height가 x축) |
728x90
'데이터 분석 (with Rstudio)' 카테고리의 다른 글
| Rstudio 사분위수(Quartile) Outliers(이상치) IQR (사분범위) (0) | 2023.07.31 |
|---|---|
| Rstudio 데이터 살펴보기 #3 (기술통계 및 데이터 분포 해석) (0) | 2023.07.30 |
| Rstudio 데이터 살펴보기 #2 (summary 함수, 결측값 확인 등) (0) | 2023.07.28 |
| Rstudio 데이터 불러오기/살펴보기 #1 (0) | 2023.07.27 |
| Rstudio 엑셀 파일 불러오기/저장하기 (0) | 2023.07.26 |



